どうも皆さんこんにちは! FkSgです。
Twitter : https://twitter.com/FkSg16KN (@FkSg16KN)
皆さんとは「7日目:webサイトやアプリの仕組み」でお会いしましたね。
今回は、Pythonで簡単なシミュレーションを1つ行いたいと思います。
シミュレーションとは、ご存知の通り「現実世界で起きた現象や事象を模擬すること」です。
今回は、ロボットやゲームのキャラクタといった複数の関節や骨を持つ構造の物体や絵柄の動き方をコンピュータ上で再現していきます。
具体的には、その中でも計算や再現が比較的簡単な
関節の角度を与えたときの手先の位置を求める(=順運動学)のシミュレーションをしました。
環境
OS:Windows10、言語:Python(バージョン3.8)、ライブラリ:numpy、matplotlib

python 文法など覚える必要性があることが少なく直観的に記述することができる。
公式サイト、ダウンロード https://www.python.org/downloads/
numpy ベクトル、内積を初め様々な数値計算を高速でできる。
公式サイト https://numpy.org/
ダウンロード https://pypi.org/project/numpy/
matplotlib 点や線をはじめ関数のグラフなどを描画できる。
公式サイト https://matplotlib.org/
ダウンロード https://pypi.org/project/matplotlib/
取り扱った物体の構造

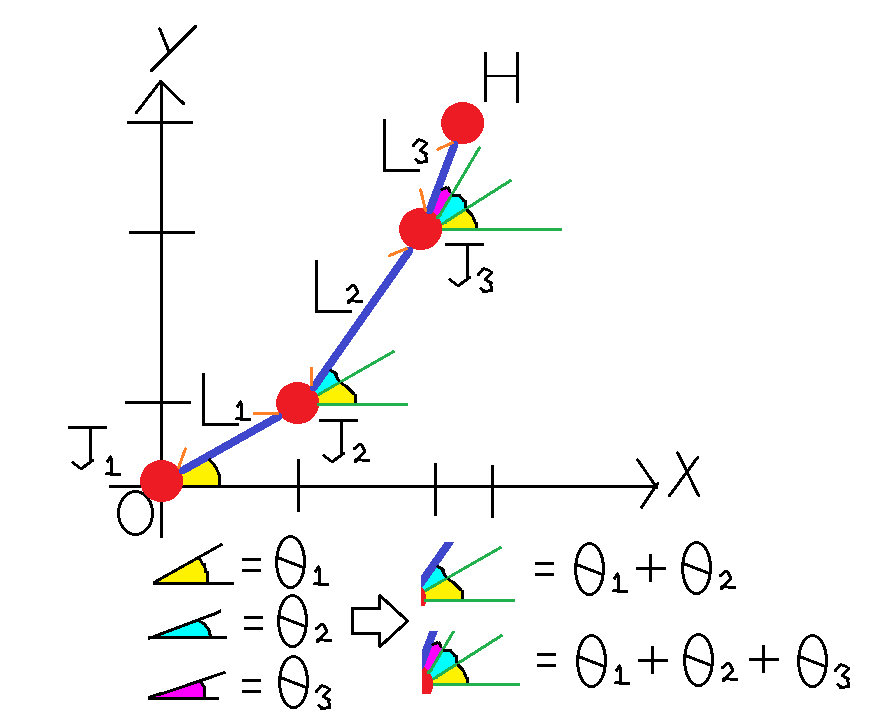
関節1=原点(0, 0)に固定 (肩の関節に相当)
関節2=骨1と骨2を繋ぐ (肘の関節に相当)
関節3=骨2と骨3を繋ぐ (手首の関節に相当)
手先=骨3の先 (指先に相当)
3つの関節と3つの骨から成るxy平面上で動作する3リンクマニピュレータ(=腕)です。
関節1、2、3と手先の角度をθ1、θ2、θ3とし、座標ベクトルをJ1、J2、J3、Hとします。
骨1、2、3の長さをL1、L2、L3とします。
(※ 関節の角度 = 1つ前の根本の骨から見た相対的な関節の角度 ≠ x軸とのなす角
角度を大きくすると骨がその関節を軸に反時計周りに回転することに注意!)
今回は、その物体がどんな姿勢をしているかを視覚的に知るために手先だけでなく他の関節の位置や骨と原点を知る必要性があります。
⇒ある関節の位置(xとyの座標)と角度(x軸との成す角)を
求めたい関節よりも根元に位置する関節の角度で表すことを考えます。
また、計算しやすくするために関節や手先の位置を原点から位置ベクトルと考えています。
解析的な考え方
関節1の場合を早速考えてみましょう!
これは定義通りなので簡単ですね。
従って、位置はJ1 = [0, 0]^Tです。
関節2の場合を考えてみましょう!
x軸と角度θ1をなす大きさL1のベクトルをxとyといった座標軸方向に分解するには?
そうですね。皆さんが高校の時の学習した三角関数を使うとできます。
半径L1の円の上にある点の座標を角度θ1を使って表すことを考えます。
x座標はL1cosθ1で、y座標はL1sinθ1となりますね。
従って、位置はJ2 = [L1cosθ1, L1sinθ1]^Tです。
関節3の場合を同様に考えてみましょう!
先ほど求めた1つ根元(=関節1)の位置から角度θ1+θ2をなす大きさL2のベクトルが伸びています。関節1で既にθ1だけ回転し、追加的に関節2でθ2だけ回転しています。
従ってx座標から見ると回転角が累積され、その角度はθ1+θ2になります。
まず、半径L2の円の上にある点の座標を角度θ1+θ2を使って表すことを考えます。
この円上の点の座標は一般的に、[L2cos(θ1+θ2), L2sin(θ1+θ2)]^Tとなります。
また、円の中心が[L1cosθ1, L1sinθ1]^Tであり平行移動させるたものであるため
円上の点の座標に円の中心の座標が足したものになります。
従って、位置はJ3 = [L1cosθ1+L2cos(θ1+θ2), L1sinθ1+L2sin(θ1+θ2)]^Tです。
最後に手先の位置も同様に考えましょう!
1つ根元は? 皆さんお分かりの通り関節2です。
そこから伸びるベクトルの角度と大きさは?
そう、角度がθ1+θ2+θ3で大きさがL3です。
後はこのベクトルを関節2の位置ベクトルに足せば求まります。
従って、
位置はH=[L1cosθ1+L2cos(θ1+θ2)+L3cos(θ1+θ2+θ3),L1sinθ1+L2sin(θ1+θ2)+L3sin(θ1+θ2+θ3)]^Tです。
実装とアルゴリズム
次にこれをPythonで記述してみましょう!
1つ目に(入力:関節の角度、出力:関節や手先の位置)となる関数を考えます。
よく式を見ると法則性が見えると思います。
一般化するために根元から見てn番目の関節nの位置を考えます。
i = 1のとき
x座標は0、y座標は0
i > 1のとき
x座標はL1cosθ1+L2cos(θ1+θ2)+ … +Ln-1cos(θ1+θ2+ … +θn-1)
y座標はL1sinθ1+L2sin(θ1+θ2)+ … +Ln-1sin(θ1+θ2+ … +θn-1)
と表すことができます。
i > 1のときプログラミングする上で反復処理に落とし込むために∑で表現すると、
x座標は∑(i=1, n-1)[Licos(∑(j=1, i) [θj])]
y座標は∑(i=1, n-1)[Lisin(∑(j=1, i) [θj])]
となりますね。
実装上では
–初期化–
1. 関節の角度のリスト、骨の長さリスト、関節の数を受け取ります。
2. 関節の位置を保持するためのリストを作ります。
–三重ループ–
3. 1つ目のループで関節の位置ベクトルの合計値を関節の位置のリストに追加します。
4. 2つ目のループで関節の位置ベクトルの合計値を求めます。∑(i=1, n-1)に相当
5. 3つ目のループで関節角の合計値を求めます。∑(j=1, i)に相当
–終了–
6. 最後に関節の位置のリストを返します。
<numpyの解説>
numpy.sin()関数 弧度法の角度を引数に代入した際の正弦を返します。
numpy.cos()関数 弧度法の角度を引数に代入した際の余弦を返します。
numpy.array()関数 numpyの配列を返します。
numpy.pi 円周率
使い方########################################################################
import numpy as np #ライブラリをインポートします。
print(np.sin(0)) #0.0と表示されます。
print(np.cos(np.pi)) #-1.0と表示されます。
print(np.array((1, 2))) #[1, 2]と表示されます。
#########################################################################
2つ目に(入力:関節の位置の座標、出力:運動物体の形状のグラフ)となる関数を考えましょう。
グラフの描画に良く用いられるのはmatplotlibというライブラリです。
今回はその物体を点や線分といった抽象的なグラフとして描画します。
–初期化–
1. グラフの初期設定、アスペクト比を1:1にします。
2. x、y座標をプロットするためのリストを作ります。
–反復処理1–
3. 関節の位置をx座標をxのリストへ、y座標をyのリストへ追加します。
–途中–
4. 太さ3、青色の線分で「骨」を描画します。
–反復処理2–
5. 大きさ15、赤色の点で「関節」を描画します。
–終了–
6. x、y座標の範囲を最も伸ばした際の形状の2倍の範囲にします。
<matplotlibの解説>
ax.plot()関数 点や直線などをグラフ上に描画します。
ax.set_xlim()関数 x軸の範囲を指定します。
ax.set_ylim()関数 y軸の範囲を指定します。
plt.show()関数 グラフを表示します。
使い方####################################################################
import matplotlib.pyplot as plt #ライブラリのインポートします。
fig = plt.figure() #描画領域全体をインスタンス化します。
ax = fig.add_subplot(aspect=1) #1つの軸や目盛りの領域をアスペクト比1:1にします。
ax.plot([0, 1], [2, 3], lw=3, color=’b’) #(0, 2)と(1, 3)を結ぶ青色の太さ3線分を描画します。
ax.plot(0, 2, marker=’.’, markersize=15, color=’r’) #(0, 2)に赤色の大きさ15の点を描画します。
ax.set_xlim([-4, 4]) #x軸を-4から4までの範囲に設定します。
ax.set_ylim([-4, 4]) #y軸を-4から4までの範囲に設定します。
plt.show() #これまでの全てのプロットをグラフに表示します。
############################################################################
3つ目にプログラム全体の関数を考えましょう!
–初期化–
1. 骨の長さ、関節の数、関節角度のパターンのリストを作ります。
–反復処理(二重ループ)–
2. 1つ目のループで、関節の角度のパターン数(今回は3パターン)だけ描画します。
3. 2つ目のループで、得られた関節の位置を文字で出力します。
初期値#######################################################################
link_lens = [0.2, 0.3, 0.1] #3つの骨でそれぞれの長さをこのように設定します。
joint_num = 3 #関節の数です
joint_args_list = [[0, 0, 0], [np.pi/2, np.pi/4, 0], [np.pi, 0, np.pi/6]] #角度のパターンリストです。
############################################################################
実行結果
横軸がx座標、縦軸がy座標、中央が原点(0, 0)を表しています。
中央(原点)に位置するのが一番根元の関節1(赤丸)です。
そこから外側にいくにつれて、
骨1(青線)、関節2(赤丸)、骨2(青線)、関節3(赤丸)、骨3(青線)、手先(赤丸)となります。
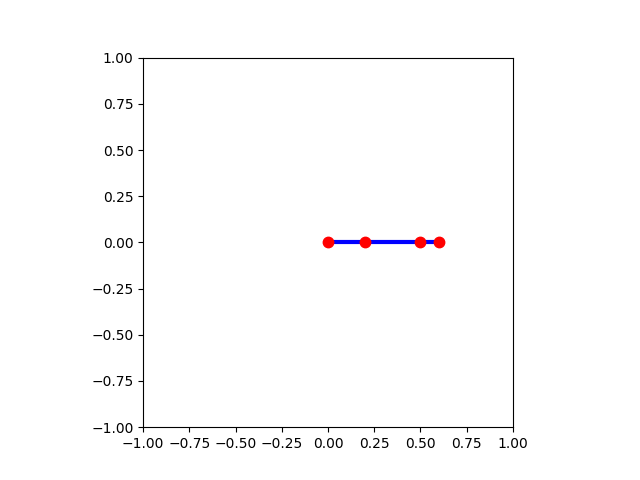
関節1、2、3の角度 0、 0、 0 [rad]
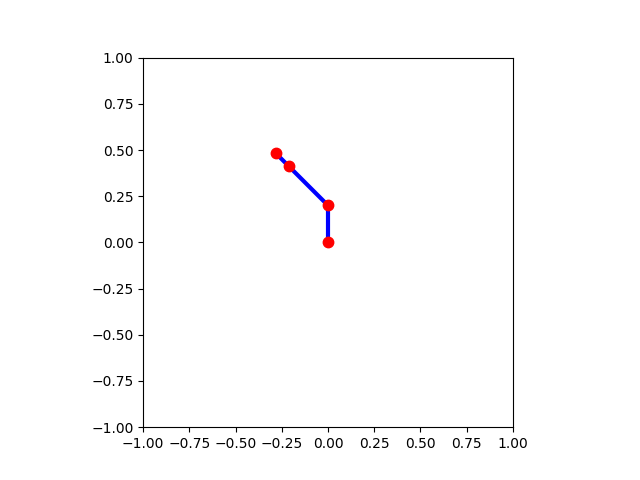
関節1、2、3の角度 π/2、π/4、0 [rad]
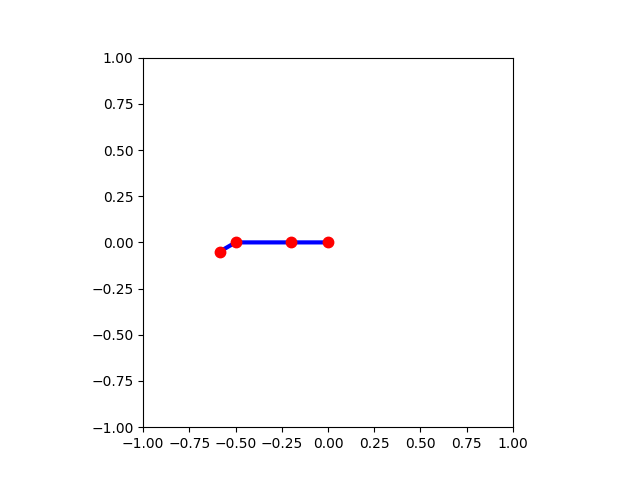
関節1、2、3の角度 π、 0、 π/6[rad]
今後の展開
自作ゲームでは、Unityでは自動的に計算されますが、
Pythonのpygameというライブラリで
人や動物といった複数の関節と骨からなるキャラクタを動かすゲームを作る際に、
姿勢を形作るために応用できます!
例えば、今回のシミュレーションの1つ目の関節の角度から関節や手先の位置を求める関数を、
キャラクタの腕や足の関節の位置を求めるために使い回すことができます。
あとは、その場所に腕や足の画像や絵を張ると動くキャラクタの完成です。
ロボットアームを動かす場合には、順運動学で位置を推定したり、
手先の位置が与えられた際の関節の角度を求める逆運動学を数値的に実装する上で
必要なヤコビ行列を記述するために応用したいと思いました!
このように、よく使われているnumpyやmatplotlibといったライブラリや
骨の長さと関節角度の和を引数とする三角関数の和で表現される簡単な式で実装でき、
ゲームやロボットなど幅広い分野で応用が利くので皆さんも作ってみてはいかがでしょうか。